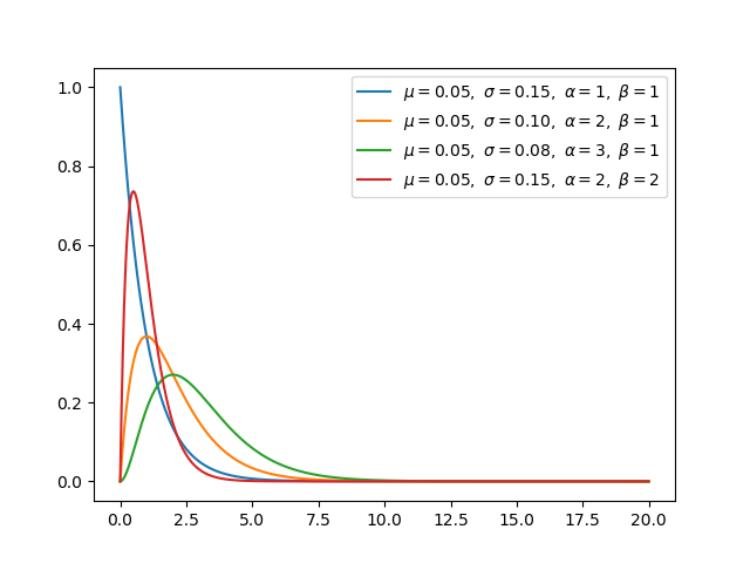
证明：指数分布的密度函数为
f(x)=λe^-λx （x>0）
=0 （x≤0）
对于s>0 ， t>0
P(X>s+t | X>s)=P(X>s+t)/P(X>s)
=∫λe^-λxdx / ∫λe^-λxdx ，积分上限为无穷 , 下限为s+t与s
=-e^[-λ(s+t)] / -e^(-λs)
=e^-λt
P(X>t)=∫λe^-λxdx (从t到无穷)
=e^-λt
=P(X>s+t | X>s)
所以命题得证。
扩展资料
无记忆性
指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布。
当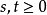 
时有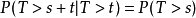
即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少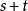 
小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。
分位数
参数λ的四分位数函数（Quartile function）是：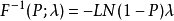
第一四分位数：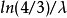 
中位数：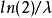 
第三四分位数：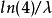 
参考资料：百度百科-指数分布
